Feldspat und Quarz orientiert verwachsen

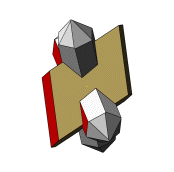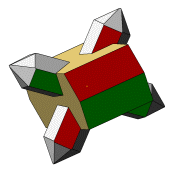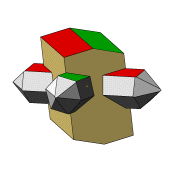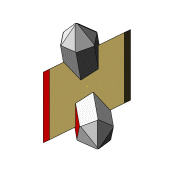
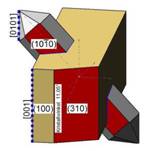
Bei den Abbildungen zu dieser Doppelreihe steht die Zone [001] am Orthoklas rechtwinklig zur Bildschirmebene und die b-Systemachse zeigt dabei nach rechts. Die Animation links zeigt beim Stopp diese Stellung.

Seit 2006 werden auf verschiedenen Börsen Mineralienstufen u.a. mit Feldspat und Rauchquarz aus Namibia angeboten. Beim Betrachten mehrerer Stufen weckten die vielfältigen Verwachsungen mein Interesse. Oft können an solchen Stufen orientierte Reihen von Quarzkristallen beobachtet werden. Auffallend ist auch, dass die aufgereihten Quarzkristalle überwiegend tafelig ausgebildet sind und die Tafeln in gleicher Richtung wie die Reihen der Quarze stehen. Bei Gesprächen mit Sammlerfreunden über die offensichtlich orientierten Verwachsungen wurden sehr unterschiedliche Meinungen geäußert. Auch konnte ich hierzu keine Literatur mit eindeutigen Aussagen finden.

Bei Ramdohr(1968) fand ich den entscheidenden Hinweis für eine mögliche Gesetzmäßigkeit. Ramdohr erwähnt dort Stufen aus Namibia mit ähnlichen Verwachsungen zwischen Orthoklas und Quarz. In den Skizzen zur „Erklärung dieser Verwachsung“ ist die Orientierung nach Punkt A im Stereogramm dargestellt. Gilt also für die hier gezeigten Stufen das gleiche Gesetz, das von Fersmann(1928) für den Schriftgranit beschrieben wurde?

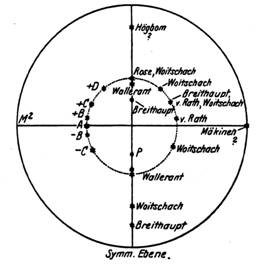
Stereographische Projektion des Feldspates (Orthoklas) mit eingetragenen Verwachsungsgesetzen. Die Punkte A bis D repräsentieren die von Fersmann gefundenen Verwachsungsgesetze. Auf der rechten Seite des Stereogramms sind weitere Autoren aufgeführt.

Die c–Systemachse des Quarzes schließt bei jeder beliebigen Drehung um die c-Systemachse des Feldspates mit dieser einen Winkel von 42°16’ ein und bildet so in der Projektion einen Kreis.

Trapezoedergesetz oder Fersmann‘sches Gesetz

Auszug aus Fersmann(1928, Seite79):

„ ... allgemeines Gesetz der Verwachsung, welches durch die parallele Orientierung der Prismenkante des Feldspates und der Kante zwischen zwei benachbarter Rhomboederflächen des Quarzes bestimmt wird. Dieses Gesetz, welches ich Trapezoedergesetz genannt habe, ruft das Zusammenfallen der Prismenzone des Feldspates mit derjenigen schrägen trapezoedrischen Zone des Quarzes hervor, in welcher zwei Prismenflächen und vier Rhomboederflächen liegen.“

Zwei Beispiele: links die Orientierung nach Punkt A; rechts die Orientierung nach Punkt –B im Stereogramm.

Im Bild steht die c-Achse des Orthoklas senkrecht auf der Bildebene.

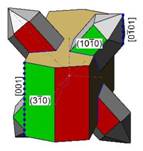
Bei allen gemusterten Stufen verliefen bei den in Reihen gegenüberliegenden Quarzkristalle keine Prismenflächen parallel zueinander. Daher kann die Orientierung, wie von Ramdohr(1968) oder Beyer(1980) beschrieben, hier nicht zutreffen. Bei der Interpretation ergab die Orientierung nach Punkt–B im Stereogramm die genauesten Ergebnisse. Ausgelegt ist diese Orientierung wie links dargestellt: die Fläche(310) und Kante[001] am Feldspat liegen parallel zur Prismenfläche(10.0) und Kante[01.1] am Quarz. Der Kristallwinkel (100):(310) beträgt 11,05°.

Bezieht man die Symmetrieebene (010) am Orthoklas in die Betrachtung mit ein, dann ergibt sich noch eine zweite mögliche Orientierung wie im Bild rechts ergänzt.

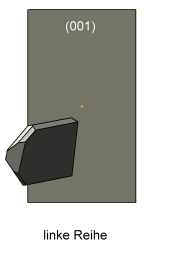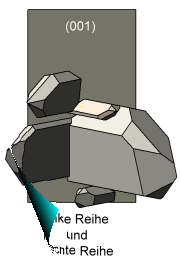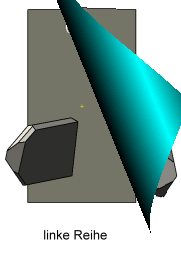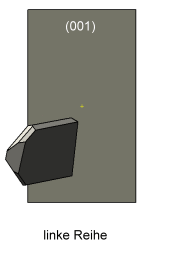
Die Prismen der aufgereihten Quarzkristalle sind mehrheitlich tafelig ausgebildet. Die linke Reihe ist nach dem Punkt–B im Stereogramm orientiert - die rechte Reihe spiegelbildlich orientiert zur Linken. Zudem stehen die Quarzkristalle in jeder Reihe parallel zueinander. Die Symmetrieebene der Doppelreihe liegt parallel zur Ebene(010) am Orthoklas. Der Schnittwinkel zwischen den gegenüberliegenden Tafelflächen beträgt rechnerisch 87,1°.

Der Interpretation zu Grunde gelegte Orientierung

Orthoklas(310)[001]

Quarz (10.0)[01.1].

Orthoklas(3-10)[001]

Quarz (10.0)[0-1.1].

1.Reihe

2.Reihe

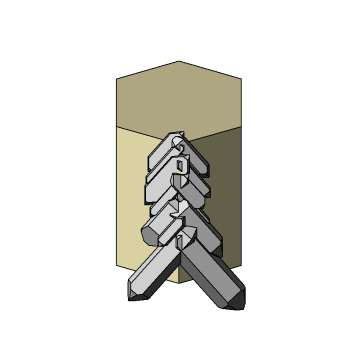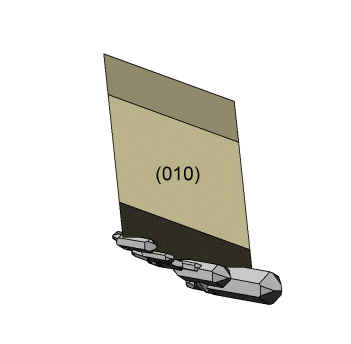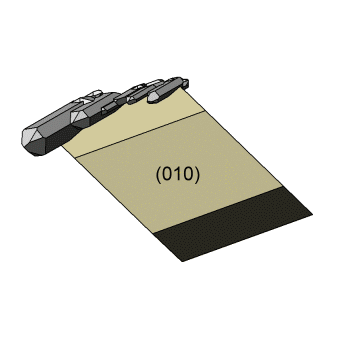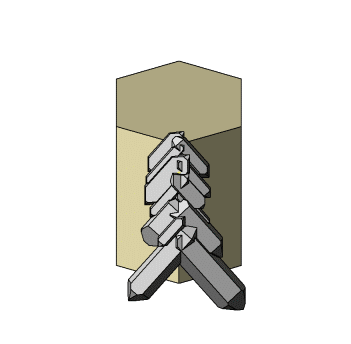
Auf den Darstellungen zu dieser Doppelreihe steht die Zone [012] am Orthoklas rechtwinklig zur Bildschirmebene und die Zwillingsebene liegt parallel zur senkrechten Bildschirmachse. Die kleine Animation links stoppt in dieser Stellung.

Die Kristalle der linken Reihe hier entsprechen den Kristallen der rechten Reihe der zuvor beschriebenen Doppelreihe. Betrachtet man die Quarzkristalle der 1.Reihe (Doppelreihe) auf einem Bavenoer Zwilling, dann entspricht die Stellung der Quarzkristalle auf der rechten Seite der Doppelreihe hier, der Orientierung nach Punkt–B im Stereogramm. Die Symmetrieebene der Doppelreihe liegt parallel zur Zwillingsebene(021) am Orthoklas. Der Schnittwinkel zwischen den gegenüberliegenden Tafelflächen beträgt rechnerisch 9,27°.

3.Reihe

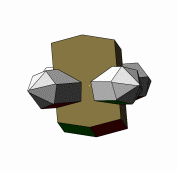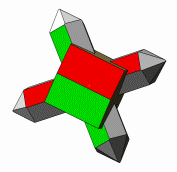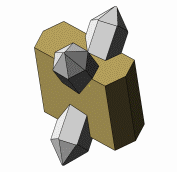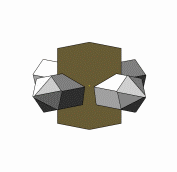
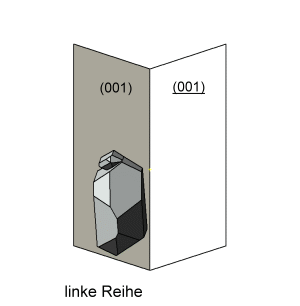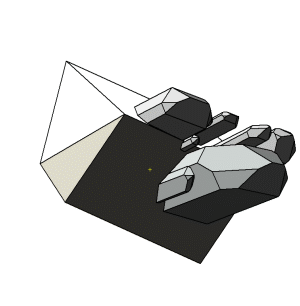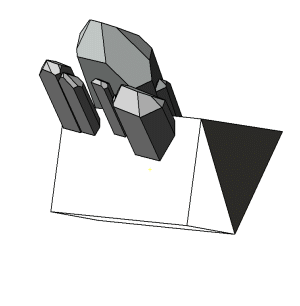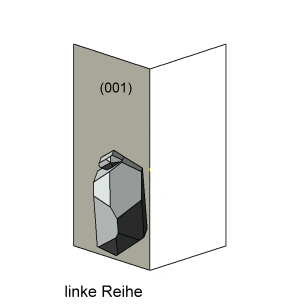
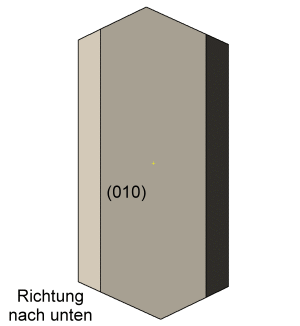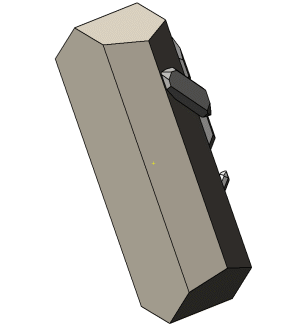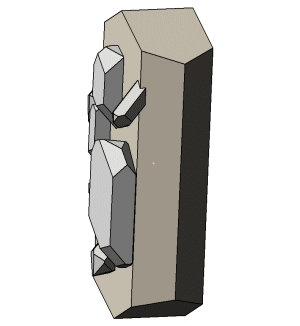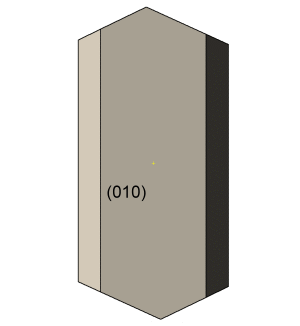
Die Abbildungen zu diesen Reihen sind so gewählt, dass die b-Systemachse am Orthoklas zum Betrachter und die c-Systemachse nach oben zeigt. In dieser Ausrichtung stoppt die kleine Animation links.

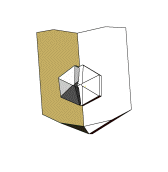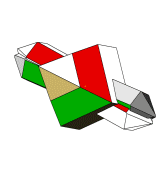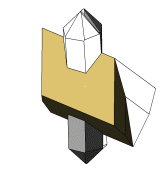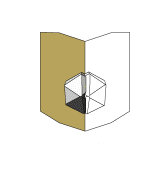
Die c-Systemachse der Quarzkristalle ist auf den Abbildungen nach unten oder nach oben gerichtet. Die Kristalle derselben Richtung sind parallel verwachsen und teilweise aufgereiht. Bei einer Blickrichtung auf (010) am Orthoklas sind die nach unten gerichteten Quarzkristalle nach Punkt–B im Stereogramm orientierten. Die Stellung der nach oben gerichteten Kristallen entspricht der zweiten Orientierung. Bei einer Betrachtung in Blickrichtung [010] am Orthoklas wechselt die Orientierung der nach oben bzw. unten geneigten Quarzkristalle.

4.Reihe

Die Stufe ist in den Abbildungen so ausgerichtet, dass die Fläche (100) am Orthoklas in der Bildschirmebene liegt und die b-Systemachse am Orthoklas nach rechts zeigt. Beim Stopp steht die kleine Animation links in dieser Ausrichtung.

Die Stufe zeigt an der vorderen bzw. hinteren Kante des Prismas {hk0} am Orthoklas aufgereihte Quarzkristalle. Auffallend bei solchen Reihen ist, dass relativ kleine Quarzkristalle sich exzentrisch durchkreuzen und so die vordere bzw. hintere Kante des Prismas am Orthoklas abzeichnen.

Die Zeichnung links zeigt eine dem Foto rechts nachempfundene Aufreihung der Quarzkristalle. Die Quarzkristalle auf der rechten Seite der Doppelreihe sind nach Punkt-B im Stereogramm orientiert.

Textfeld: Die beiden Stufen habe ich in den angegebenen Aufstellungen fotografiert und dann die Reihen der Quarzkristalle, auf den Fotos als Hintergrund, mit Kristall2000 nachgezeichnet. Für alle Zeichnungen zu den vier Reihen ist dieselbe Orientierung ausgelegt.

Literatur

Beyer, Heinz (1980): Mineralbeobachtungen an der kleinen Spitzkopje (SW-Afrika). der Aufschluss 31 (1980) 4-32

Fersmann,A.E. (1928): Die Schriftstruktur der Granitpegmatite und ihre Entstehung. Zeitschrift für Kristallographie 69 (1929) 77-104

Koritnig, S. (1983): Schriftgranit. der Aufschluss 34 (1983) 527-533.

Ramdohr, P. (1968): Aus meinen mineralogisch-geologischen Reisen Teil I- Namibia-Südafrika. der Aufschluss 19 (1968) 79-88.

Ramdohr, P. & Strunz, H. (1980): Klockmanns Lehrbuch der Mineralogie. 521,773.

Schilling, Klaus (2009): Feldspat und Quarz orientiert verwachsen aus Namibia. der Aufschluss 60 (2009) 231-235

Fazit:

Aktives Mineral im Sinne von Fersmann - hier „richtunggebend“ für den Quarz - ist der Orthoklas. Die interpretierten Reihen sind so betrachtet je ein Merkmal derselben Orientierung zwischen Orthoklas und Quarz wie oben beschrieben. Im Umkehrschluss bieten sich weitere reizvolle Betrachtungen an, z.B.: zeigt die 2.Reihe einen Bavenoer Zwilling an und die 4.Reihe gibt einen Hinweis zur Aufstellung des Feldspatkristalls auf dem sie gewachsen ist.