2015 und 2016 fand Jürgen Greiner bei Üdersdorf, Hillesheim und Hinterweiler in der Eifel interessante Nephelin-Kristalle - davon zwei Beispiele auf Bild 01 und 02. Bei Gesprächen mit Sammlerfreunden wurde wiederholt spontan die Ausbildung als Zwillinge angesprochen. Leider war in der Literatur (Betechtin 1971; Goldschmidt 1920, Hintze 1897; Ramdohr&Strunz 1978) und den deutschen Sammlermagazinen keine Beschreibung zur Morphologie dieser Zwillinge zu finden.

Nachfolgend eine Beschreibung von Nephelinvierlingen nach {00.1} und {11.0} und weiter zwei Methoden, die die Einschätzung der Beispiele in Bild 01 und 02 als Zwillinge nach {31.0} stützen.

Bild 01: Nephelin-Zwilling nach {31.0} - BB 2,0 mm

Steinbruch Graulay, Hillesheim

©Foto und Sammlung: Jürgen Greiner

Bild 02: Nephelin-Zwilling nach {31.0} - BB 2,1 mm

Steinbruch Feuerberg, Hinterweiler

©Foto und Sammlung: Jürgen Greiner

Kristall2000 | Arbeitsweise | Anwendungen | Grundlagen | Historie | Informationen | Oberfläche | Schaufenster | Vorträge | Zwillinge

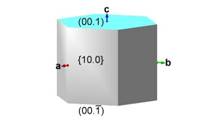
Bild 03: hypothetischer Einzelkristall

mit drei Kristallformen

Standardaufstellung

In der Eifel zeigt sich Nephelin an mehreren Fundstellen als frei gewachsene einfache hexagonale Säulen. Betrachtet man diese als Einzelkristalle, dann entspricht die Morphologie - in der Kristallklasse (6) angesprochen - einer Kombination aus drei Kristallformen (Bild 03): dem Prisma {10.0}, dem oberen Basispedion (00.1) und dem unteren Basispedion (00.-1).

Diese Kristalle treten jedoch stets als Doppelzwillinge nach {00.1} und {11.0} auf.^{.(1, 5)}

Nephelin: hexagonal-pyramidale Klasse (6), a:c = 1:0.839 ⁽⁵⁾

Bild 04: hypothetischer  Zwilling

nach {00.1}

mit zwei Kristallformen

Bild 06: idealer Vierling nach

{00.1} und {11..0}

Standardaufstellung

Anschließend ist die Morphologie für einen Nephelin-Vierling in 3 Schritten entwickelt.

Bild 08: idealer Zwilling im Programm Kristall2000 orientiert auf das Foto aufgelegt; die gemessenen Schnittwinkel sind rot eingetragen

Literatur

⁽¹⁾ Betechtin, A.G. (1971): Lehrbuch der speziellen Mineralogie. 627-629, VEB Verlag für Grundstoffindustrie Leipzig.

⁽²⁾ Goldschmidt, V. (1920): Atlas der Kristallformen. Band VI 80-83 Tafel 45-46, Reprint 1986

⁽³⁾ Hintze, C. (1897): Handbuch der Mineralogie. Band II 853-872, Verlag von Veit&Comp. Leipzig.

⁽⁴⁾ Niggli, P. (1941): Lehrbuch der Mineralogie und Kristallchemie. 408, Verlag von Gebrüder Bornträger Berlin-Zehlendorf.

^(5).Ramdohr, P. & Strunz, H. (1978): Klockmanns Lehrbuch der Mineralogie. 767-768, Ferdinand Enke Verlag Stuttgart.

 

Greiner, J. & Schilling, K. (2017): Zur Morphologie von Nephelinkristallen aus der Eifel. DER AUFSCHLUSS 68 (6/2017) 337-342

1.Schritt

Der hypothetische Zwilling nach {00.1} erscheint als mimetischer Zwilling. Der Zwilling simuliert eine Kombination aus zwei Kristallformen (Bild 04): dem Prisma {10.0} und dem Basispinakoid {00.1}. Die niedrigere Symmetrie ist nur durch Ätzfiguren und röntgenografisch erkennbar.^{.(1, 5)}

Die Zwillingsebene teilt die Prismenflächen {10.0} waagrecht.

3.Schritt

Ein Zwilling nach {00.1} und {11.0} wird als Kontaktzwilling z.B. durch die vierfache Lage von unsymmetrischen Ätzfiguren auf den Prismenflächen deutlich. Auf Bild 06 sind die Abschnitte der Individuen idealisiert dargestellt. Die verschieden platzierten idealisierten Ätzfiguren sollen die vier Individuen hervorheben. Beim realen Kristall durchdringen sich die Individuen mit unregelmäßigen Grenzen.^{.(1, 5)}

2.Schritt

Beim hypothetische Zwilling nach {11.0} teilt die Zwillingsebene die Flächen des Prismas {10.0} senkrecht.

Bild 05: hypothetischer Zwilling

nach {11.0}

Auf den Bildern 01 und 02 sind augenscheinlich Zwillinge abgebildet. Diese Einschätzung wird durch gleiche Merkmale an mehreren Beispielen auch von verschiedenen Fundorten bestärkt (Niggli 1941).

Dazu zwei Methoden, die diese Annahme glaubhaft erscheinen lassen.

Tabelle: rechnerische Schnittwinkel zwischen den Individuen

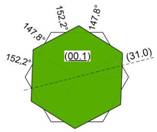
1.Methode

Zum Vergleich wurden Beispiele mit den Kristallflächen (00.1) und (00.1) parallel zur Bildebene fotografiert und dann die Schnittwinkel (wie auf Bild 08 rot eingetragen) zwischen den Individuen gemessen. Auffallend dabei war der umlaufend regelmäßige Wechsel von zwei verschiedenen Winkeln (siehe dazu Bild 07). Die Durchschnittswerte aller gemessenen Winkel betrugen 152,9° bzw. 147,5°. Auch die geringen Unterschiede der äquivalenten Winkel bei den verschiedenen Beispielen wiesen auf eine gesetzmäßige Verwachsung hin.

Nun galt es ein Zwillingselement zu finden, das die gemessenen Winkel bestätigt. Eine Zwillingsachse [00.1] ist ausgeschlossen, da diese - bei einer Drehung eines Individuums um 180° - die beiden Individuen wieder deckungsgleich abbildet.

Hier sollte nun der Weg über Versuch und Irrtum weiter helfen. In der Tabelle sind für eine fortlaufende Folge von hypothetischen Zwillingsebenen (hk.l) die rechnerischen Schnittwinkel zwischen den Individuen zusammen gestellt. In der zweiten Spalte der Tabelle stehen die rechnerischen Schnittwinkel die links am Individuum in Zwillingsstellung (im Bild 07 grün dargestellt) ermittelt wurden. Sinngemäß stehen in der dritten Spalte die gegenüber liegenden Schnittwinkel.

Die Ergebnisse in der zweiten Zeile entsprechen - mit geringen Differenzen - den gemessenen Schnittwinkeln. Damit erscheint hier das Zwillingsgesetz {31.0} als wahrscheinlich.

Bild 07: idealer Zwilling nach {31.0} mit den rechnerischen Schnittwinkeln zwischen den Individuen

2.Methode

Für einen weiteren Vergleich wurden die Fotos, die auch als Grundlage für die Vermessung dienten, im Programm Kristall2000 als Hintergrund eingelesen und der ideale Zwilling zum realen Zwilling orientiert aufgelegt (Bild 08). Nun konnten im Programm durch Verschieben die Kanten des idealen Kristalls mit den entsprechenden Kanten am realen Kristall zur Deckung gebracht werden. Da alle äquivalenten Kanten - bei derselben Orientierung - zur Deckung gebracht werden konnten, wird auch mit diesem Vergleich die Annahme bekräftigt, dass auf den Bildern 01 und 02 Zwillinge nach {31.0} abgebildet sind.