Anlass zur Ausarbeitung dieser Seite gab mir ein Artikel in der MINERALIENWelt 18 (3) 24 - 31 und 19 (6) 36 - 51 mit dem Titel:„Mineralien aus der Eifel: Zwillingsbildungen, Epitaxien und Pseudomorphosen“. Der Artikel enthält mehrere Darstellungen zur Kristallmorphologie, die an Hand von Fachliteratur nicht nachzuvollziehen sind. Studieren Sie die folgende Betrachtung zur Morphologie von Zwillingskristallen, vergleichen Sie und urteilen Sie selbst.

 

Um Missverständnissen oder gar Fehlern bei der Arbeit mit Kristall2000 vorzubeugen, sollen hier die Anwendungsmöglichkeiten der Zwillingselemente an Beispielen problematisiert werden.

 

Zwillingskristalle nach Klockmann(1980, Seite 72)

„Zwillingskristalle sind zwei nach einem zusätzlichen Symmetrieelement miteinander verwachsene Individuen der gleichen Kristallart, …. . Als zusätzliches Symmetrieelement = Zwillingselement kann morphologisch eine Symmetrieebene = „Zwillingsebene“ oder eine Digyre = „Zwillingsachse“ auftreten (bei azentrischen Kristallen vielleicht auch ein Inversionszentrum).“

 

Diskussion zur Anwendung der Zwillingselemente dargestellt an Beispielen

Die Vorgabe soll ein Fluoritzwilling mit zwei Würfeln als Idealkristalle sein. Nachgezeichnet aus Klockmann(1980, Seite 72). Ein Individuum ist farblos, das zweite in Zwillingsstellung grün dargestellt. Fluorit kristallisiert im kubischen Kristallsystem in der Hex‘oktaedrischen Klasse (m3m).

Eine Zwillingsachse als Zwillingselement am Fluorit ?

In der Animation wird das grüne Individuum fortlaufend um 10° gedreht. Als Drehachse ist passend zur Vorgabe die Diagonale von vorn-unten-rechts nach hinten-oben-links gewählt. Diese Diagonale entspricht im kubischen Kristallsystem der Richtung [11-1] oder [-1-11].

Verfolgen Sie in der Animation die Stellung der Individuen bei 60, 120, 180, 240, 300 und 360°. Beachten Sie dabei auch die Lage der Systemachsen zueinander.

Nach Klockmann(1980), Seite 9 sind theoretisch zwei-, drei-, vier– und sechszählige Drehachsen als Symmetrieelemente möglich. Das entspricht einer Schrittweite für den Drehwinkel von 2 mal 180°, 3 mal 120°, 4 mal 90° bzw. 6 mal 60°. In der Animation erscheint nur bei einem Drehwinkel von 60°, 180° und 300° eine Zwillingsstellung wie in der Vorgabe gezeigt. Bei den Drehwinkeln 120, 240 und 360° stehen die zwei Individuen deckungsgleich zueinander.

Nach Augenschein kann hier eine zweizählige Drehachse (180°), eine vierzählige Achse (hierbei nur bei 180°) oder eine sechszählige Achse (hierbei nur bei 60, 180 und 300°) als Zwillingselement nur vermutet werden.

Hinweis: In der Kristallklasse m3m ist eine dreizählige Achse [111] als Symmetrieelement vorhanden !

Eine Zwillingsebene als Zwillingselement am Fluorit ?

Für den Fluorit gilt nach Klockmann(1980), Seite 72 ff. das Spinellgesetz {111}. Dieses Gesetz ergibt, als Kristallform betrachtet, in der Kristallklasse m3m das Oktaeder. Die acht Flächen des Oktaeders können als Zwillingselemente betrachtet werden. So gesehen ist theoretisch der Zwilling, wie oben vorgegeben, in acht unterschiedlichen Aufstellungen möglich. Diese acht Aufstellungen lassen sich durch Drehungen in deckungsgleiche Lagen bringen.

Die Fläche (11-1) ist das Zwillingselement zur Vorgabe

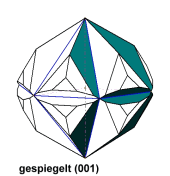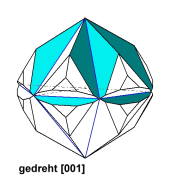
In den nachfolgenden animierten Bildern sind je zwei Abbildungen übereinander gelegt. Weiter ist an den Individuen je Bild die gleiche Kristallfläche koloriert. Durch den fortlaufenden Wechsel der Bilder wird deutlich, dass die Abbildungen geometrisch gleich sind. Jedoch erscheinen die kolorierten Flächen zueinander je nach angewandter Symmetrieoperation in verschiedenen Lagen - achten Sie auch auf die Systemachsen. Das heißt, dass die Individuen zueinander verschieden aufgestellt sind. Welche Aufstellung davon ggf. richtig ist, kann der Anwender von Kristall2000 nach Augenschein nur mit morphologischen Merkmalen (Symmetrie von Ätzfiguren, Spaltrisse u.a.) oder mit Fachliteratur belegen.

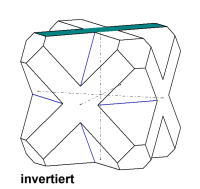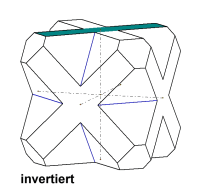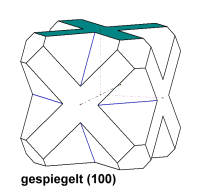
Ein Beispiel aus dem kubischen System.

Die Fläche (001) ist koloriert, sie erscheint gespiegelt (100) vereinigt oben, invertiert oben und unten (unsichtbar).

Die Lage der Systemachsen verändert sich.

Aus dem trigonalen System ein Beispiel.

Die Fläche (0kl) ist koloriert, sie erscheint gedreht [001] nur oben, gespiegelt (001) oben und unten.

Die Lage der Systemachsen verändert sich.

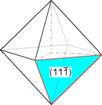
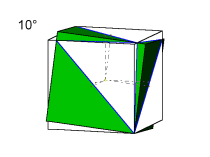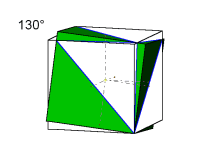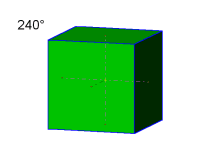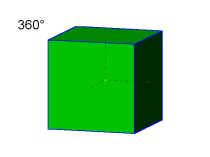
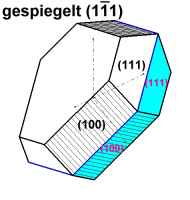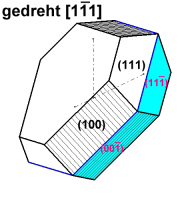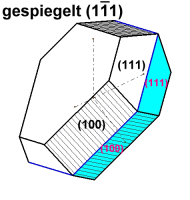
Hierzu das konkrete Beispiel: ein Zinkblendezwilling mit den Formen {100} und {111} nachgezeichnet nach Klockmann(1980). Als morphologisches Merkmal sind die Würfelflächen schraffiert. Im animierten Bild sind eine nach dem Gesetz {111} gespiegelte und eine nach dem Gesetz [111] gedrehte Abbildung übereinander gelegt. Im Bildwechsel wird deutlich, dass die Abbildungen geometrisch zwar gleich sind, die Würfelflächen aber verschieden zueinander aufgestellt sind. Im Klockmann(1980, Seite 426) gilt als Zwillingsgesetz die „Zwillingsachse[111]; bei diesem Gesetz sind die Zwillingshälften mit positivem und negativem Tetraeder aneinandergewachsen“.

Eine alte Weisheit aktualisiert: Man darf nicht alles glauben was in der Zeitung steht oder weil es mit dem Computer geht!

Weiterführende Literatur finden Sie auf der Seite Informationen.

Beispiele: Faujasit-Kontaktzwillinge nach dem Spinellgesetz {111}

Fotos und Sammlung: Volker Betz , 65232 Taunusstein

Die Bilder wurden mit Kristall2000 bearbeitet und befinden sich auf der CD.

Bitte beachten Sie hierzu auch den Faujasit-Drilling im Schaufenster !

Kristall2000 | Arbeitsweise | Anwendungen | Grundlagen | Historie | Informationen | Oberfläche | Schaufenster | Vorträge | Zwillinge